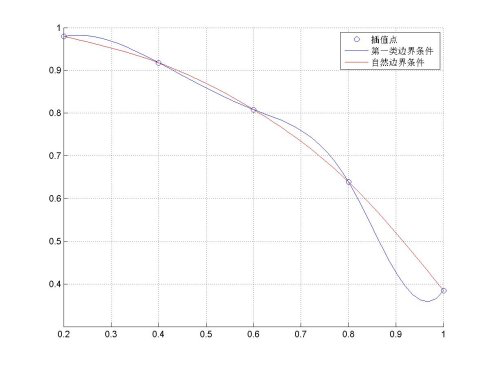
三次样条差值（MATLAB）

function sanciytchzh
% made by louis 2009/06/12
promps={'请输入插值点:'};
result=inputdlg(promps,'插值点x=',1,{'[ 0.2000    0.4000    0.6000    0.8000    1.0000]'});
x =str2num(char(result));
promps={'请输入插值点对应的函数值f(x)='};
result=inputdlg(promps,'插值点处函数值',1,{'[0.9798652 0.9177710 0.8080348 0.6386093 0.3843735]'});
y =str2num(char(result));
promps={'请输入边界条件:'};
result=inputdlg(promps,'第一类边界条件',1,{'[ 0.20271,1.5574]'});
s2=str2num(char(result));
promps={'请输入边界条件:'};
result=inputdlg(promps,'第二类边界条件',1,{'[ 0,0]'});
s1=str2num(char(result));
hold on
grid on
plot(x,y,'o');
a1=diyi(x,y,s2);
a2=ziran(x,y,s1);
for i=1:length(a1)
disp(['第一类边界条件的弯矩M',num2str(i)','为：',num2str(a1(i))]);
end
for i=1:length(a1)
disp(['自然边界条件的弯矩M',num2str(i)','为：',num2str(a2(i))]);
end
legend('插值点','第一类边界条件','自然边界条件');
function M=diyi(x,y,s)
%made by louis 2009/06/12
%第一类边界条件的三次样条插值
g1=chashang(x,y);
h=x(2:length(x))-x(1:length(x)-1);
for i=1:length(h)-1
    u(i)=h(i)/(h(i)+h(i+1));
    r(i)=1-u(i);
end
g(1)=6/h(1)*(g1(1,1)-s(1));
g(2:length(x))=6*g1(2,:);
g(length(x))=6/h(length(h)-1)*(s(2)-(y(length(y))-y(length(y)-1))/h(length(h)));
A=2*eye(length(g));
for i=2:length(g)-1
    A(i,i+1)=r(i-1);
    A(i,i-1)=u(i-1);
end
A(1,2)=1;
A(length(g),length(g)-1)=1;
M=zhuigan(A,g);
h(2:length(h)+1)=h;
n=50;%选取50个插值点
x1=[min(x):(max(x)-min(x))/(n-1):max(x)];
for i=1:n
    m=x(1);
    for k=2:length(x)
        if x1(i)<=m+h(k);
            y1(i)=M(k-1)*(x(k)-x1(i))^3/(6*h(k))+M(k)*(x1(i)-x(k-1))^3/(6*h(k))+(y(k-1)-M(k-1)*h(k)^2/6)*(x(k)-x1(i))/h(k)+(y(k)-M(k)*h(k)^2/6)*(x1(i)-x(k-1))/h(k);
            break;
        end
        m=m+h(k);
    end
end
plot(x1,y1)
function M=ziran(x,y,s2_1)
% made by louis 2009/06/11
% 满足自然条件的三次样条插值
g=chashang(x,y);
g=6*g(2,:);
g(length(x)-1)=[];%把g的最后一个零去掉，因为这个0并不是所算出的二阶差商
h=x(2:length(x))-x(1:length(x)-1);
for i=1:length(h)-1
    u(i)=h(i)/(h(i)+h(i+1));
    r(i)=1-u(i);
end
g(1)=g(1)-u(1)*s2_1(1);
g(length(g))=g(length(g))-r(length(r))*s2_1(1);
A=2*eye(length(g));
for i=1:length(g)-1
    A(i,i+1)=r(i);
    A(i+1,i)=u(i+1);
end
M(2:length(x)-1)=zhuigan(A,g);
M(length(x))=0;
h(2:length(h)+1)=h;
n=50;%选取50个插值点
x1=[min(x):(max(x)-min(x))/(n-1):max(x)];
for i=1:n
    m=x(1);
    for k=2:length(x)
        if x1(i)<=m+h(k);
            y1(i)=M(k-1)*(x(k)-x1(i))^3/(6*h(k))+M(k)*(x1(i)-x(k-1))^3/(6*h(k))+(y(k-1)-M(k-1)*h(k)^2/6)*(x(k)-x1(i))/h(k)+(y(k)-M(k)*h(k)^2/6)*(x1(i)-x(k-1))/h(k);
            break;
        end
        m=m+h(k);
    end
end
plot(x1,y1,'r');
function fc=chashang(x,y)%求差商
% made by louis 2009/06/08
format long
clc
n=length(x);
l=length(y)-1;
for i=1:n-1
    for j=1:l
        fc(i,j)=(y(j+1)-y(j))/(x(j+i)-x(j));
    end
    clear y;
    y=fc(i,:);
    l=l-1;
end
function X=zhuigan(A,B)%追赶法解方程组
% made by louis 2009/06/08
clc
[L,U]=lu(A);
n=length(B);
y(1)=B(1);
for i=2:n
    y(i)=B(i)-L(i,i-1)*y(i-1);
end
x(n)=y(n)/U(n,n);
for i=n-1:-1:1
    x(i)=(y(i)-U(i,i+1)*x(i+1))/U(i,i);
end
X=x;