常用的图形变换
坐标系
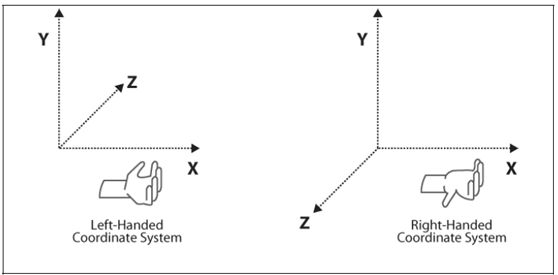
坐标系在开发过程中常分为世界坐标系和屏幕坐标系 通常我们的坐标系采用右手型,下图展示了左手坐标系和右手坐标系的区别
- 左手坐标系，伸出左手用大拇指指向方向轴的方向，其余4个手指自然弯曲，则4指弯曲方向为角度变化的正方向
- 右手坐标系和左手坐标系对称，只需将左右换成右手即可
- iOS采用的是左手坐标系
向量的变换
图像上每个点的位置可以看成一个向量n维向量，取决于图像的空间。所以对图像的变换可以等价于对向量的变换，研究向量的变换可以让我们更直观的了解图像变换的原理
- 向量的平移（对坐标系内某点得移动）
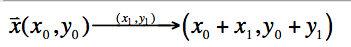
- 向量的缩放
X饭方向缩放a倍，Y方向缩放b倍，则有
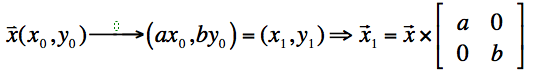
- 向量的旋转
二位平面的向量旋转，即可以表示为三维空间的向量绕Z轴的旋转
如图：
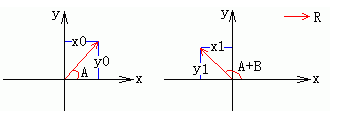将向量x在平面X-Y内绕原点旋转B，假设向量x的模为R，则根据三角函数的知识得
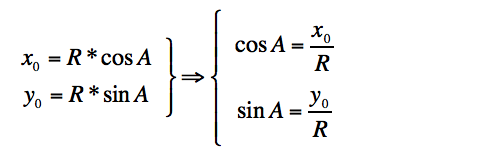,旋转后的向量为
用矩阵表达即为
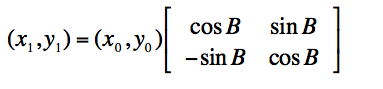
如果向量的起点不是（0，0）点，怎么推导旋转矩阵？ 假设有向量x，则可表示为两个起点为（0，0）的向量的和，则对旋转变换P有 xP=（x1+x2）P==>x1P+x2P
复杂的变换
通常我们的变换不仅局限于只做上述3个变换的一种，但是由于上述3中变换的原子性，所以所有的正交变换都可拆解为上述变换的组合
即有正交变换P
P=ABCDEFG
其中ABCDEFG位相应的正交变换
注：由于矩阵乘法不具备交换律，所以变换顺序的改变会直接改变变换的结果
三维空间的坐标变换
对上述方法进行拓展，我们很容易得出三维空间的变换矩阵
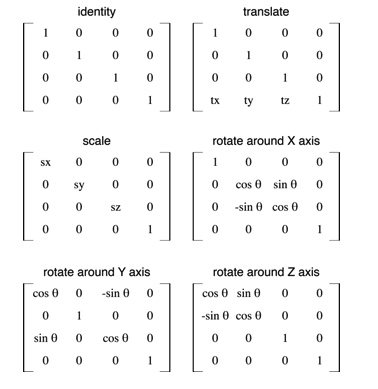
坐标系内的点绕任意向量旋转，如何处理? 可以对改点进行平移或旋转A，使改向量与任一坐标轴重合，然后针对该坐标轴进行旋转。旋转接受后，再对旋转后的做逆变换，即乘以inv（A） 举例，某点绕向量（1，1，0）进行旋转，推算旋转矩阵
图像的变换
图像可以看成一个RGB颜色的集合，通过在不同的位置显示不同颜色呈现出可识别的图案。
图像中的每个点的坐标，抽象成一个坐标矩阵，与变换矩阵做乘法，即可得出图像的变换
图像变换的逆变换
由于图像变换都可归结为矩阵的乘法，所以所有正交变换都存在逆变换，只需对变换后的图像矩阵乘以变换矩阵的逆矩阵即可。 *再次注意矩阵的乘法不具备交换率，所以必须按照顺序进行变换的消除
齐次向量
所谓齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示。例如，二维点(x,y)的齐次坐标表示为(hx,hy,h)。由此可以看出，一个向量的齐次表示是不唯一的，齐次坐标的h取不同的值都表示的是同一个点，比如齐次坐标(8,4,2)、(4,2,1)表示的都是二维点(4,2)。 为什么引入齐次坐标
齐次变换
齐次变换具有如下形式：
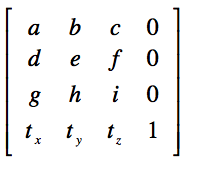对向量x做变换，有如下等式成立
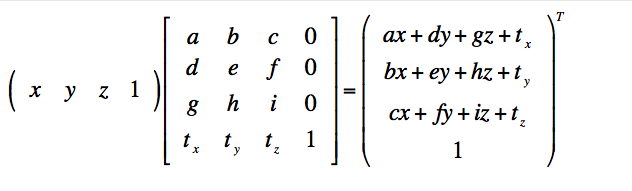当b、c、d、f、h都等于0时，a、e、i都等于1时，则有
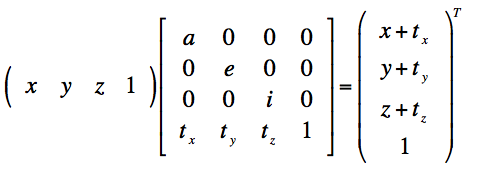对向量（坐标系）的变换一般分为，缩放、平移、旋转，引入齐次向量和齐次变换，将所有的变换统一为矩阵的乘法运算
投影
透视投影
透视投影,是为了获得接近真实三维物体的视觉效果而在二维的纸或者画布平面上绘图或者渲染的一种方法，也称为透视图[1]。它具有消失感、距离感、相同大小的形体呈现出有规律的变化等一系列的透视特性，能逼真地反映形体的空间形象。透视投影通常用于动画、视觉仿真以及其它许多具有真实性反映的方面。
透视投影的标准模型
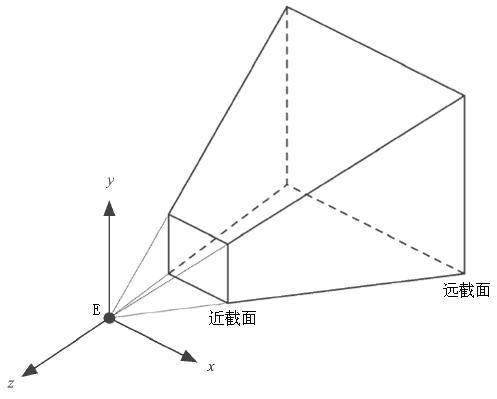推导透视投影标准模型的变换方程
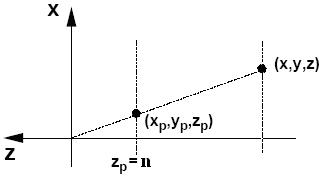
根据三角形的相似性，我们可以得出
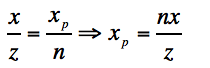有与在手机设备上，原点位于手机屏幕上，所以需要对上述公式做平移，得出针对与手机坐标系的投影关系，如下
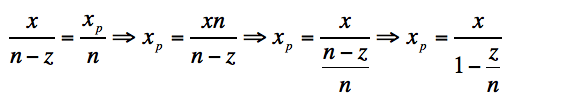同理我们可以得到，y坐标的投影为
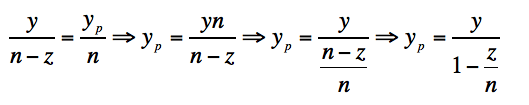注意，由于我们的视平面是屏幕，即x，y平面，所以所有z坐标在视屏幕的投影始终为0
将上述变换写成矩阵乘法的形式，我们可以的到如下的表达式
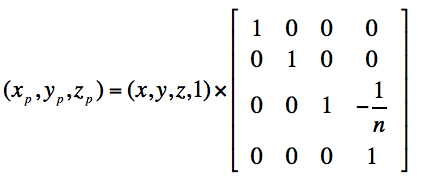
记住这个变换，后边会讲到
变换在iOS中的应用
在介绍变换在iOS中的应用前，先了解2个变量，这两个变量和iOS中transform有很大关系
- 锚点
anchorPoint anchorPoint是一个[0,1]的点，当我们对layer的postion和transform进行变换时，我们必须要考虑当前的anchorPoint值，默认情况下anchorPoint=（0.5,0.5）.下图表明了anchorPoint和postion，frame，bounds的关系
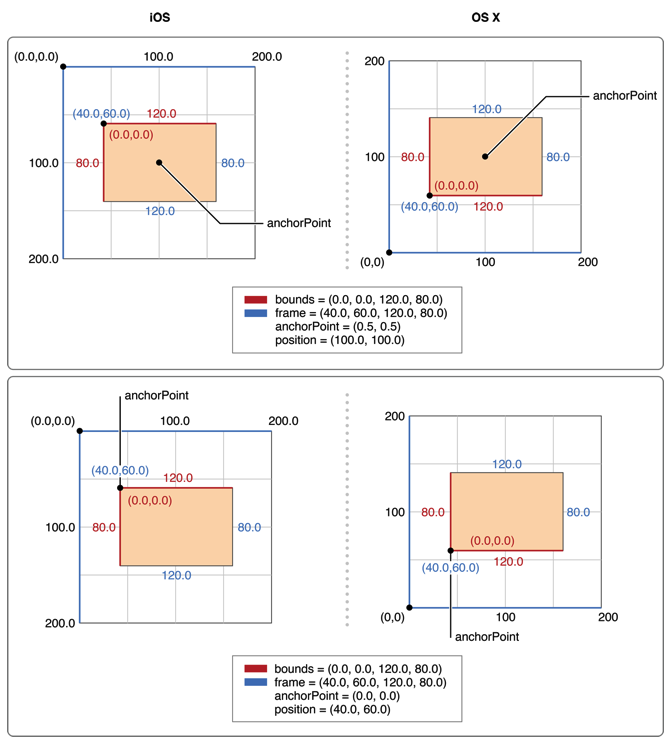我们可以将anchorPoint理解为三维系统内Z轴的位置，或者说在三维空间中z轴的位置，当anchorPoint为（0.5，0.5）时，我们对图像做旋转变换，即是以图像的中心点为基准进行旋转。当anchorPoint为（0，0）时，则这个中心点则变为图像的左上角
如下图：
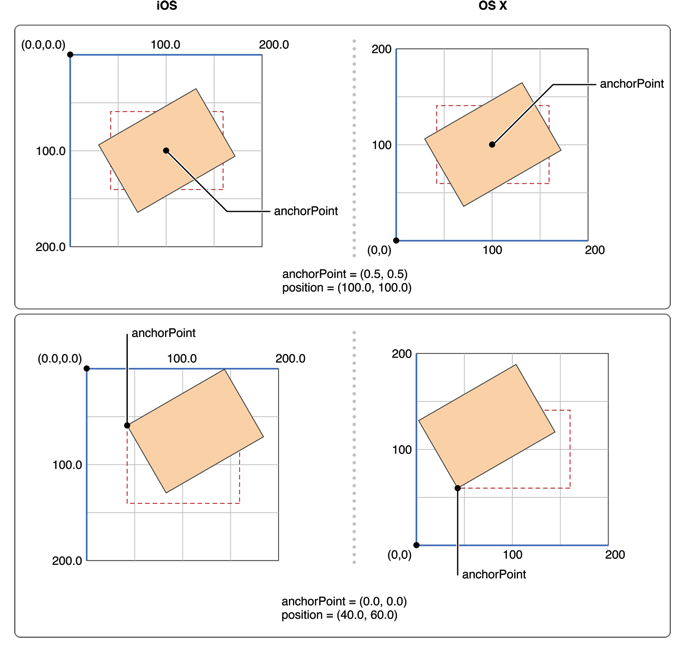
- 代码展示 下面的代码与系统自身生成变换矩阵得出的结论一致
//平移，x方向移动100px
- (CGAffineTransform)moveTransform
{
CGAffineTransform transform = CGAffineTransformIdentity;
transform.tx = 100;
transform.ty = 0;
return transform;
}
//平移，x方向移动100px
- (CATransform3D)moveTransform3D
{
CATransform3D transform = CATransform3DIdentity;
transform.m41 = 100;
return transform;
}
//缩放,x,y方向放大2倍
- (CGAffineTransform)scaleTransform
{
CGAffineTransform transform = CGAffineTransformIdentity;
transform.a = 2;
transform.d = 2;
return transform;
}
//缩放,x,y，z方向放大2倍
- (CATransform3D)scaleTransform3D
{
CATransform3D transform = CATransform3DIdentity;
transform.m11 = 2;
transform.m22 = 2;
transform.m33 = 2;
return transform;
}
//旋转，绕z轴正方向旋转alpha
- (CGAffineTransform)rotationTransform
{
double alpha = -M_PI / 4;
CGAffineTransform transform = CGAffineTransformIdentity;
transform.a = cos(alpha);
transform.b = sin(alpha);
transform.c = -sin(alpha);
transform.d = cos(alpha);
return transform;
}部分如片来源于网络